There is great uncertainty about future climate change and its associated economic impacts. To ensure effective policy, it is important that models try to account for the impact of human activity on climate change, and in turn, how climate affects human activity. Econometric models can and have been successfully used for this, but models estimating these links have to be supported by empirical evidence and the underlying climate physics.

In a new paper published in the Journal of Econometrics I show how (simple) climate system models can be estimated using econometric methods consistent with physical processes. Formally, the paper shows that energy balance models – which analyse the energy budget of the Earth to estimate climate change – are mathematically equivalent to an econometric cointegrated system and can be estimated as such.

Why is this useful?

It is imperative to understand the relationship between the economy and climate in order to make informed decisions as to the best way to respond. Economic damages of climate change have been conventionally assessed using integrated assessment models (such as Nordhaus’ DICE model). These models internally rely on energy balance models to describe how the climate responds to different emissions and policies. However, integrated assessment models conventionally do not consider uncertainties on important climate parameters because they are difficult to estimate jointly. My approach can provide uncertainties on those parameters and subsequently be used to provide projections of the economic damages of climate change.

Beyond integrated assessment models, recent work quantifying the economic impacts of climate change has turned towards empirical models. However, the empirical field of estimating climate-econometric models is split in two. One side models economic activity conditional on climate, such as economic growth as a function of temperatures. While the other side models temperatures conditional on radiative forcing stemming in-part from greenhouse gas emissions and thus underlying economic activity. Each side makes assumptions about what the other side tackles, not testing for the potential presence of bi-directional feedbacks and adjustment. My approach provides a stepping-stone in addressing this, allowing for a full-system estimation, albeit on a global scale. This can move us towards an empirical system model of climate affecting the economy and economy affecting the climate.

Applying the Methods

Using the mathematical equivalence of a climate model and econometric system, I find that time series observations of global mean surface temperatures, ocean heat content, and radiative forcing form stationary relations consistent with the underlying theory. In other words, there is strong empirical support for the model quantifying the effect of human-induced (anthropogenic) greenhouse gas concentrations on both temperatures and ocean heat content.

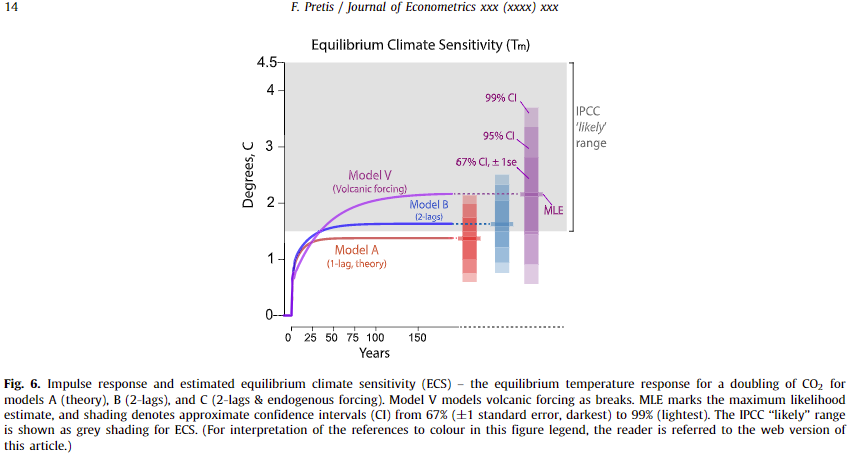
The resulting model provides estimates of the Equilibrium Climate Sensitivity (ECS, the equilibrium temperature response to a doubling of CO­₂ concentrations), and shows that previous empirical estimates of the ECS may be artificially low due to model mis-specification and not modelling atmosphere-ocean dynamics. Accounting for structural breaks (induced by volcanic eruptions and perhaps El Nino), the “best estimate” in the paper suggests an ECS of 2.13C, which is higher than many empirical estimates and provides further empirical support of the IPCC likely range (mostly derived from simulated climate models) – see Figure 6 taken from the paper below. There is also evidence of some short-run feedback from temperatures back onto radiative forcing from anthropogenic sources.

More generally, the mathematical equivalence between econometric methods and climate-processes provides a physical science foundation for the use of cointegration methods to study climate responses – it places the entire econometric time series toolkit at the disposal of empirical climate-economic models while being consistent with the underlying physics.

 Felix Pretis, Co-Director Climate Econometrics, University of Victoria